Chap.4 La radioactivité

 

Introduction : la découverte de la radioactivité

Voici un rappel des dates qui ont marqué une étape dans la connaissance de la radioactivité.

1895 : le physicien allemand Wilhelm Röntgen découvre les rayons X.

1896 : le physicien français Henri Becquerel découvre la radioactivité lors de ses travaux sur la phosphorescence. Il constate qu'un sel d'uranium émet un rayonnement appelé rayonnement uranique, à la fois semblable et plus complexe, que celui du rayonnement X.

1897 : la physicienne française d'origine polonaise Marie Curie (née Maria Sklodowska) commence, en décembre, l'étude du rayonnement uranique.

1898 : Marie Curie et son mari Pierre Curie, étudient la pechblende, un minerai d'oxyde d'uranium très riche en rayonnement, et découvrent 2 nouveaux éléments chimiques, qu'ils appelleront le polonium (en l'honneur de la nation d'origine de Marie) et le radium (car cet élément est fortement radioactif). Marie Curie invente le mot "radioactivité".

Pierre et Marie Curie, Henri Becquerel et Ernest Rutherford, font l'expérience que les rayonnements radioactifs peuvent être déviés par un champ électrique ou un champ magnétique. Ils montrent que le rayonnement `α` est constitué de particules "lourdes" et chargées positivement, et que le rayonnement β est constitué de particules "plus légères" et chargées négativement qui seront rapidement identifiées aux électrons.

1900 : le physicien Français Paul Villard découvre le rayonnement gamma.

1908 : le physicien néo-zélandais Ernest Rutherford montre que les particules `α` sont des noyaux d'hélium, composés de 2 protons et 2 neutrons.

1932 : le physicien américain Carl David Anderson découvre le positon (dont l'existence avait été prédite en 1928 par le physicien britannique Paul Dirac).

1934 : Frédéric Joliot et sa femme Irène Joliot-Curie (fille de Pierre et Marie Curie) découvrent que de l'aluminium bombardé par des particules `α` se transmute en un isotope artificiel radioactif du phosphore. Ils viennent d'inventer la radioactivité artificielle qui permettra de synthétiser de nombreux nucléides et de découvrir la radioactivité β⁺.

. . . . Voici une histoire sonore de Marie Curie et un dossier très complet sur son œuvre proposés par le Ministère de la recherche.

. . . . Voici la page du site Wikipédia consacrée à Marie Curie.

 

1. Noyaux atomiques

 

Le noyau d'un atome est constitué de nucléons : les protons et les neutrons.

Les protons sont des particules ayant une charge positive e = 1,602 . 10^-19 C et une masse m_p = 1,673 . 10^-27 kg.

Les neutrons sont des particules ayant une charge nulle et une masse m_n = 1,675 . 10^-27 kg.

Le nombre de nucléons d'un noyau, aussi appelé nombre de masse, est noté A.

Le nombre de protons du noyau, aussi appelé nombre de charges (ou numéro atomique de l'atome correspondant) est noté Z.

Un noyau (ou nucléide) est donc caractérisé par son nombre de nucléons A et son nombre de charges Z .

. . . . D'où la notation :

`{::}_Z^A`X

ligne

. . . . Remarque : le nombre de neutron d'un noyau est donc N = A - Z.

 

Isotopes

On appelle isotopes, des noyaux ayant même numéro atomique Z, mais des nombres de nucléons différents.

Des noyaux isotopes ont donc une masse différente, mais appartiennent au même élément chimique.

. . . . Exemples :

. . . . . . . - il existe 3 isotopes naturels de l'hydrogène : . .`{::}_1^1`H (99,985 %); . .`{::}_1^2`H (0,015 %); . .`{::}_1^3`H (moins de 0,001 %).

ligne

ligne

. . . . . . . - il existe 3 isotopes naturels du carbone : . .`{::}_6^12`C (98,89 %); . .`{::}_6^13`C (1,11 %); . .`{::}_6^14`C (moins de 0,001 %).

ligne

ligne

. . . . . . . - il existe 2 isotopes naturels du cuivre : . .`{::}_29^63`Cu (69,17 %); . .`{::}_29^65`Cu (30,83 %).

ligne

ligne

. . . . . . . - il existe 6 isotopes naturels du calcium : . .`{::}_(\20)^40`Ca (97 %); . .`{::}_(\20)^42`Ca; . .`{::}_(\20)^43`Ca; . .`{::}_(\20)^44`Ca; . .`{::}_(\20)^46`Ca; . . `{::}_(\20)^48`Ca (0,2 %).

ligne

A partir de 1934, les physiciens ont découvert de très nombreux noyaux artificiels obtenus par divers bombardements de noyaux connus.

Ainsi, ils ont montré qu'il existe environ 350 noyaux naturels et plus de 2000 noyaux artificiels différents.

L'étude de ces nombreux nucléides a montré que la majorité de ces noyaux sont instables (en particulier tous les noyaux artificiels).

. . . . Exemples :

. . . . Parmi les nucléides mentionnés ci-dessus, 3 nucléides sont radioactifs : . . .`{::}_(\1)^3`H (le tritium), . . `{::}_(\6)^14`C (le carbone 14) . .et . .`{::}_(\20)^48`Ca (le calcium 48).

En fait, les nucléons subissent dans un noyau des forces en compétition. Il y a l'interaction forte responsable de leur attraction (et donc de la cohésion du noyau), mais il y a aussi la répulsion électrique des protons.

Ainsi, selon l'intensité relative de ces 2 forces, certains noyaux sont stables, alors que d'autres sont instables.

 

Diagramme (N,Z)

Tous les noyaux connus sont représentés dans ce diagramme, où le nombre N de neutrons est en ordonnée et le nombre Z de protons est en abscisse.

. . . . Remarque :

. . . . La représentation avec N en ordonnée et Z en abscisse est plus courante que celle choisie par votre manuel, avec Z en ordonnée et N en abscisse.

Les noyaux stables sont représentés par une case noire et les noyaux instables par une case de couleur.

ligne

 

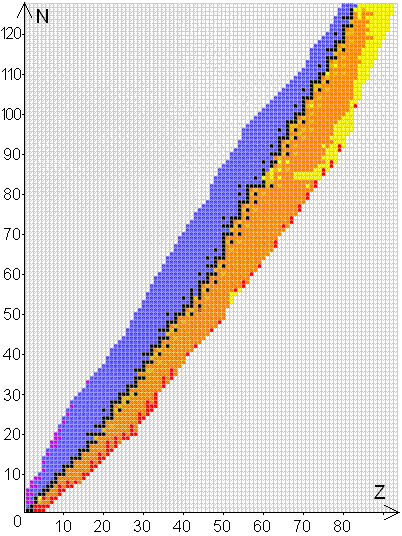
2. Radioactivité

 

Un noyau instable peut se transformer en un autre noyau en émettant une particule ou un rayonnement.

Au cours de cette transformation nucléaire, aussi appelée désintégration radioactive, il y a conservation de la charge et conservation du nombre de nucléons. On donne le nom de "lois de Soddy", à ces 2 lois de conservation.

On distingue 3 types de désintégrations radioactives : la radioactivité `α, β` et `γ`.

 

Radioactivité `α`

La radioactivité `α` est une désintégration s'accompagnant de l'émission d'un noyau d'hélium `{::}_(\2)^4`He, nommé particule `α`.

D'après les lois de Soddy, à un noyau père . .`{::}_(\Z)^A`X . .correspond un noyau fils . .`{::}_(\Z-2)^(A-4)`X' . .

. . . . D'où l'équation :

`{::}_(\Z)^A`X . .—> . .`{::}_(\Z-2)^(A-4)`X' . .+ . .`{::}_(\2)^4`He

. . . . Exemple :

`{::}_84^210`Po . .—> . .`{::}_82^206`Pb . .+ . .`{::}_2^4`He

. . . . Remarques :

. . . . . . . - Dans le diagramme (N,Z) les noyaux pouvant se désintégrer par radioactivité `α` sont représentés par des cases jaunes.

. . . . . . . - Le noyau fils obtenu par radioactivité `α` est tel que . . N' = N - 2 . .et . .Z' = Z - 2.

 

Radioactivité `β`^-

La radioactivité `β`^- est une désintégration s'accompagnant de l'émission d'un électron, nommé particule `β`^-.

D'après les lois de Soddy, à un noyau père . .`{::}_(\Z)^A`X . .correspond un noyau fils . .`{::}_(\Z+1)^A`X' . .

. . . . D'où l'équation :

`{::}_(\Z)^A`X . .—> . .`{::}_(\Z+1)^A`X' . .+ . .`{::}_(\-1)^0`e

. . . . Exemple :

`{::}_(\82)^210`Pb . .—> . .`{::}_(\83)^210`Bi . .+ . .`{::}_(\-1)^0`e

. . . . Remarques :

. . . . . . . - Dans le diagramme (N,Z) les noyaux pouvant se désintégrer par radioactivité `β`^- sont représentés par des cases bleues.

. . . . . . . - Le noyau fils obtenu par radioactivité `β`^- est tel que . . N' = N . .et . .Z' = Z + 1.

 

Radioactivité `β`⁺

La radioactivité `β`⁺ est une désintégration s'accompagnant de l'émission d'un positon `{::}_(\1)^0`e, nommé particule `β`⁺.

Le positon (appelé aussi positron ou anti-électron) `{::}_(\1)^0`e, est l'antiparticule de l'électron. Il a la même masse qu'un électron mais une charge électrique positive +e. Cette particule a été découverte tardivement car elle est détruite lors de sa collision avec un électron. Le positon et l'électron s'annihilent alors en libérant de l'énergie.

D'après les lois de Soddy, à un noyau père . .`{::}_(\Z)^A`X . .correspond un noyau fils . .`{::}_(\Z-1)^A`X' . .

. . . . D'où l'équation :

`{::}_(\Z)^A`X . .—> . .`{::}_(\Z-1)^A`X' . .+ . .`{::}_(\1)^0`e

. . . . Exemple :

`{::}_(\35)^80`Br . .—> . .`{::}_(\34)^80`Se . .+ . .`{::}_(\1)^0`e

. . . . Remarques :

. . . . . . . - Dans le diagramme (N,Z) les noyaux pouvant se désintégrer par radioactivité `β`⁺ sont représentés par des cases oranges.

. . . . . . . - Le noyau fils obtenu par radioactivité `β`⁺ est tel que . . N' = N . .et . .Z' = Z - 1.

 

Emission `γ`

L'émission `γ` est une désexcitation s'accompagnant de l'émission d'un rayonnement électromagnétique `γ`. Comme toute radiation électromagnétique, le photon `γ` émis a une masse et une charge nulles.

D'après les lois de Soddy, à un noyau père excité, noté . .`{::}_(\Z)^A`X^*, . .correspond un noyau fils désexcité . .`{::}_(\Z)^A`X . .

. . . . D'où l'équation :

`{::}_(\Z)^A`X^* . .—> . .`{::}_(\Z)^A`X . .+ . .`γ`

. . . . Exemple :

`{::}_(\84)^210`Po^* . .—> . .`{::}_(\84)^210`Po . .+ . .`γ`

. . . . Remarques :

. . . . . . . - Dans le diagramme (N,Z) les noyaux pouvant se désintégrer par émission `γ` ne sont pas représentés.

. . . . . . . - Le noyau fils obtenu par émission `γ` est tel que . . N' = N . .et . .Z' = Z.

. . . . . . . - L'émission `γ` n'est donc pas une désintégration nucléaire, mais simplement la décharge, sous forme d'un rayonnement `γ`, d'un excès d'énergie qui rendait le noyau instable.

 

3. Décroissance radioactive

 

Loi de décroissance radioactive

La désintégration radioactive d’un ensemble de noyaux instables est spontanée et aléatoire. En effet, la désintégration des noyaux étudiés ne peut ni être accélérée, ni être ralentie par des moyens physiques ou chimiques.

L'étude d'une population de noyaux radioactifs (identiques) montre qu'il est impossible de prédire le moment où un atome donné va se désintégrer, car cette désintégration est indépendante de l'âge de l'atome. Mais le comportement d'un très grand nombre d'atomes identiques suit une loi statistique, d'autant mieux vérifiée que le nombre d'atome est élevé.

Soit N(t) le nombre de noyaux radioactifs (identiques) présents dans un échantillon à l’instant t.

Les échantillons composés d'un grand nombre de noyaux radioactifs se comportent selon la loi de décroissance radioactive :

N(t) = N₀ . e^-`λ`t

. . . . Remarques :

. . . . La grandeur `λ` est appelée la constante radioactive et s'exprime en s^-1 (puisque le temps t est exprimé en s).

. . . . Cette relation est également utilisable avec le temps t exprimé en jour et `λ` en jour^-1, ou le temps t exprimé en an et `λ` en an^-1...

. . . . Les nombres N₀ et N sont considérés comme étant des "grands nombres", c'est-à-dire supérieurs à 10¹⁵ ou 10¹⁸ noyaux.

 

Soit N(t+Δt) le nombre de noyaux radioactifs présents dans un échantillon à l’instant t+Δt.

Soit ΔN la variation du nombre de noyaux radioactifs durant l'intervalle de temps Δt.

. . . . Remarques :

. . . . Comme le nombre de noyaux radioactifs diminue au cours du temps, ΔN est négatif.

. . . . ΔN = N(t+Δt) – N(t).

Le nombre noyaux qui se sont désintégrés durant l'intervalle de temps Δt est : N(t) – N(t+Δt) = - ΔN.

 

Activité d'un échantillon

On appelle activité A(t) de l’échantillon le nombre de désintégrations par seconde.

L'activité d'un échantillon donné peut être mesurée à l'aide d'un compteur Geiger (voir les descriptions donnée sur le site Wikipédia et sur un site canadien Cyberscol).

. . . . Pendant l'intervalle de temps Δt, l'activité d'un échantillon donné est égale au nombre de noyaux radioactifs désintégrés (soit - ΔN).

. . . . L'activité moyenne de cet échantillon, pendant l'intervalle de temps Δt, est : A = - `(ΔN)/(Δt)`.

L'activité instantanée de cet échantillon, à l'instant t, est : A(t) = - `lim_(\Δt —> 0)` `(ΔN)/(Δt)` = - `(dN)/(dt)`.

. . . . D'où :

A(t) = - `(dN)/(dt)`.

. . . . Or, N(t) = N₀ . e^-`λ`t, selon la loi de décroissance radioactive.

. . . . D'où, `(dN)/(dt)` = -`λ` . N₀ . e^-`λ`t = -`λ` . N(t).

. . . . D'où :

A(t) = - `(dN)/(dt)` = `λ` . N(t).

. . . . Sachant que N(t) = N₀ . e^-`λ`t, cette relation peut aussi s'écrire :

A(t) = `λ` . N₀ . e^-`λ`t = A₀ . e^-`λ`t.

. . . . Avec : . .A₀ = `λ` . N₀

L'unité de l'activité A(t) de l’échantillon (nombre de désintégrations par seconde) est le becquerel (symbole : Bq).

. . . . Remarque :

. . . . Lorsqu'on utilise la relation . .A(t) = `λ` . N(t) , . .il faut exprimer la constante radioactive `λ` en s^-1 pour avoir l'activité A(t) en Bq.

 

Demi-vie

La demi-vie t_½ d’un isotope radioactif est la durée au bout de laquelle la moitié des noyaux radioactifs de l'échantillon se sont désintégrés.

. . . . unités :

Dans le système international, l'unité de la demi-vie est la seconde, mais parfois il est plus commode de l'exprimer en heure, en jour ou en années.

. . . . Exemples :

. . . . . . . - la demi-vie de l'hydrogène `{::}_(\1)^4`H est de 899 ns ;

. . . . . . . - la demi-vie de l'azote `{::}_(\7)^16`N est de 7,13 s ;

. . . . . . . - la demi-vie du radon `{::}_(\86)^222`Ra est de 3,8 jours ;

. . . . . . . - la demi-vie du tritium `{::}_(\1)^3`H est de 12,34 ans ;

. . . . . . . - la demi-vie du carbone `{::}_(\6)^14`C est de 5,73 . 10³ ans ;

. . . . . . . - la demi-vie de l'iode `{::}_(\53)^129`I est de 15,7 . 10⁶ ans ;

. . . . . . . - la demi-vie du potassium `{::}_(\19)^40`K est de 1,28 . 10⁹ ans ;

Selon les nucléides considérés, la valeur de la demi-vie peut aller de la nanoseconde au milliards d'années.

 

Soit N₀ le nombre de noyaux radioactifs (identiques) présents dans un échantillon.

Quelles que soient les valeurs, du nombre initial de noyaux radioactifs N₀ et de leur demi-vie t_½, le graphe N(t) est une courbe exponentielle de la forme suivante :

 

 

D'après la définition de la demi-vie t_½, on a :

N(t_½) = `N_0` . e^-`λ`.t½ = `(N_0)/2`

. . . . D'où :

e^-`λ`.t½ = `1/2`

. . . . D'où :

e^`λ`.t½ = 2

. . . . D'où :

`λ` . t_½ = ln 2

. . . . D'où :

t_½ = `(ln 2)/λ`

 

Une application extrêmement importante de la loi de décroissante radioactive est la possibilité de dater des spécimens anciens d'os, de bois, de pierre ... Les exercices 4C et 4D précisent la méthode utilisée.

Une autre application, utilisée en chimie, en géologie, ou en médecine, est d'utiliser des molécules contenant un atome radioactif comme traceurs. Cela permet, par exemple, suivre le trajet de ces molécules dans l'organisme humain. On peut ainsi observer, sans avoir besoin d'opérer, le fonctionnement d'organes tels que le coeur, les reins, le foie, ou même le cerveau.

 

. . . . Remarque :

. . . . Pour un nucléide donné, il existe une autre durée caractéristique, appelée la constante de temps `τ`. C'est la durée de vie moyenne des noyaux. La valeur de cette constante est :

t_½ = `1/λ`

. . . . En effet, la durée de vie moyenne des noyaux est plus grande que la demi-vie pour un nucléide donné.

 

Sur le site du Commissariat à l'Energie Atomique, vous pourrez trouver plusieurs dossiers sur la radioactivité :

. . . . . . . - la radioactivité (définition, origine et applications) ;

. . . . . . . - les rayonnements (origine, effet sur l'organisme, protection et applications) ;

. . . . . . . - l'imagerie médicale (outils et applications) ;

. . . . . . . - les questions souvent posées ...