Exercice 4B
Enoncé :
Un ressort à spires non jointives de raideur k = 25 N.m-1 a une longueur à vide lo = 20 cm.
Son extrémité supérieure est fixe et un objet de masse m = 200 g est accroché à son extrémité inférieure.
a. Représenter le diagramme objets-interactions pour l'objet de masse m.
b. Représenter le schéma des forces appliquées à l'objet de masse m.
c. Calculer la longueur l du ressort lors de cet équilibre.
d. Donner les caractéristiques de la force exercée par l'objet sur le ressort.
. . . . . . . Donnée :. . g = 10 N.kg-1.
Solution :
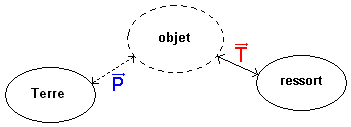
a. Le diagramme objets-interactions pour l'objet :
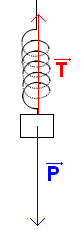
L'objet est soumis à 2 forces : son poids `vec{P}` et la tension du ressort `vec{T}`.
b. Schéma des forces appliquées à l'objet de masse m :
c. D'après la première loi de Newton, l'objet étant en équilibre (Δ`vec{v}` = `vec{0}`), la somme vectorielle des forces appliquées est nulle.
Or, l'objet de masse m étant en équilibre sous l'action des 2 forces `vec{P}` et `vec{T}`, ces forces sont telles que :
`vec{P}` + `vec{T}` = `vec{0}`
. . . . . . . D'où :
`vec{P}` = - `vec{T}`
Les 2 forces `vec{P}` et `vec{T}` ont donc :
. . . . . . . - même direction (verticale) ;
. . . . . . . - même intensité (T = P) ;
. . . . . . . - sens opposés.
Or le poids `vec{P}` de l'objet est tel que :. . P = m . g
. . . . . . . A.N. : . . P = 0,200 . 10 = 2,0 N.
. . . . . . . D'où : . . T = P = 2,0 N.
Or la tension `vec{T}` est telle que :. . T = k . (l-lo)
. . . . . . . D'où : . . (l-lo) = `T/k`
. . . . . . . D'où : . . l = lo + `T/k`
. . . . . . . A.N. : . . l = 0,20 + `2/(25)` = 0,28 m = 28 cm.
d. D'après la troisième loi de Newton, la force exercée par l'objet sur le ressort est telle que : `vec{F}`objet/ressort = - `vec{F}`ressort/objet
Or la force exercée par le ressort sur l'objet est égale à la tension `vec{T}` du ressort.
. . . . . . . D'où :
`vec{F}`objet/ressort = - `vec{T}`
Or, d'après la question précédente :
`vec{P}` = - `vec{T}`
. . . . . . . D'où :
`vec{F}`objet/ressort = `vec{P}`
La force exercée par l'objet sur le ressort est donc égale au poids `vec{P}` de cet objet.