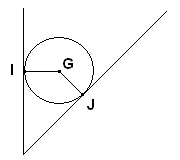Exercice 3C

 

Enoncé :

 

Une sphère de centre G et de masse 0,5 kg est immobile dans une cannelure dont le fond est horizontal.

On suppose qu'il n'y a aucun frottement lors de cet équilibre.

 

 

a. Représenter le diagramme objets-interactions pour la sphère.

b. Représenter le schéma des forces appliquées à la sphère.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Solution :

 

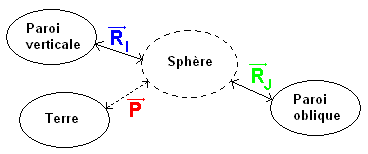
a. Le diagramme objets-interactions pour la sphère :

 

 

 

La sphère subit 3 interactions : une interaction à distance avec la Terre et deux interactions de contact avec les parois.

La sphère est donc soumise à 3 forces : son poids `vec{P}` et les réactions `vec{R_I}` et `vec{R_I}` des parois.

Donnons d'abord les caractéristiques de ces 3 forces.

 

Le poids `vec{P}` :

. . . . . . . - direction : verticale

. . . . . . . - sens : descendant

. . . . . . . - valeur : P = m g ; . . . . A.N. :. .P = 0,50 . 10 = 5,0 N.

 

La réaction `vec{R_I}` :

. . . . . . . - direction : horizontale car la réaction est normale (perpendiculaire à la paroi) puisqu'il n'y a aucun frottement

. . . . . . . - sens : de I vers G

. . . . . . . - valeur : R_I à déterminer.

 

La réaction `vec{R_J}` :

. . . . . . . - direction : selon la droite GJ car la réaction est normale (perpendiculaire à la paroi) en l'absence de frottements

. . . . . . . - sens : de J vers G

. . . . . . . - valeur : R_J à déterminer.

 

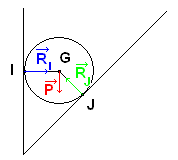
b. Schéma des forces appliquées à la sphère :

 

 

La sphère étant en équilibre sous l'action de 3 forces non parallèles, nous obtenons 2 conditions concernant ces forces.

 

1ère condition : Les forces `vec{P}` , `vec{R_I}` et `vec{R_J}` sont concourantes, c'est-à-dire que les droites d'action de ces 3 forces se coupent en un point unique.

La figure est bien en accord avec cette condition, puisque les directions des 3 forces passent par le point G.

 

2ème condition : `vec{P} + vec{R_I} + vec{R_J} = vec{0}`

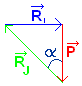
Cette condition peut être représentée par le triangle des forces.

 

 

Chaque vecteur-force étant représenté avec sa direction et son sens, les grandeurs des vecteurs sont alors proportionnelles aux 3 côtés du triangle rectangle obtenu.

 

Pour trouver les valeurs des réactions, il suffit d'exprimer les relations trigonométriques applicables à ce triangle.

 

. . . . . . . tan α = `R_I/P` ;. . . . d'où : . . R_I = P . tan α

. . . . . . . A.N. : . . R_I = 5,0 . tan 45 = 5,0 N.

 

. . . . . . . cos α = `P/R_J` ;. . . . d'où : . . R_J = `P/(cos α)`

. . . . . . . A.N. : . . R_J = `(5,0)/(cos 45)` = 7,1 N.

 

Pour visualiser un équilibre sous l'action de 3 forces, voici une représentation trouvée sur le site d'un professeur allemand M. Walter Fendt. Là on peut faire varier les valeurs des différentes forces et vérifier que la résultante des forces est nulle, en construisant le parallélogramme des forces.