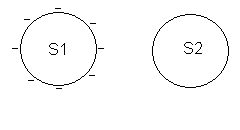D.S.1 du 01/10/10
1a. Calcul de la masse molaire de l’aspirine : . . MAsp = 9 MC + 8 MH + 4 MO
. . . . . . A.N. : . . MAsp = 9 . 12 + 8 . 1 + 4 . 16 = 180 g.mol-1
Calcul de la quantité de matière de l’aspirine : . . nAsp = mAsp/ MAsp
. . . . . . A.N. : . . nAsp = (500 . 10-3)/180 = 2,78 . 10-3 mol.
1b. Calcul de la concentration de l’aspirine dans l’eau : . . cAsp = nAsp/ V
. . . . . . A.N. : . . cAsp = `(2,78 . 10^-3)/(0,100)` = 2,78 . 10-2 mol.L-1
1c. D’après la relation des gaz parfaits, la pression du dioxyde de carbone est telle que pV = nCO2RT ;
. . . . . . D'où : . . nCO2 = `(pV)/(RT)`
. . . . . . A.N. : . . nCO2 = `((1,0 .10^5) . (70 . 10^-6))/((8,31)(273+25))` = 2,8 . 10-3 mol = 2,8 mmol.
2. Calcul de la quantité de matière de l’acide acétique : . . nAA = c . V
. . . . . . A.N. : . . nAA = 2,0 . 100 . 10-3 = 2,0 . 10-1 mol.
Calcul de la masse de l’acide acétique dissous : . . mAA = nAA . MAA
. . . . . . A.N. : . . mAA = 2,0 . 10-1 . 60 = 12 g.
Calcul du volume de l’acide acétique à prélever : . . mAA = ρ . V
. . . . . . D'où : . . V = mAA / ρ
. . . . . . A.N. : . . V = `12/(1,08)` = 11,1 . 10-3 L = 11,1 mL.
3a. Calcul des quantités de matière initiales :
Quantités de matière initiales d'oxyde de cuivre : . .nCuO = mCuO/ MCuO
. . . . . . A.N. : . . nCuO = `(1,00)/(63,5 + 16)` = 1,26 . 10-2 mol.
Quantités de matière initiales de carbone : . .nC = mC/ MC
. . . . . . A.N. : . . nC = `(0,120)/12` = 1,00 . 10-2 mol.
3b. Equation de la réaction : . . . . . C + 2 CuO `to` CO2 + 2 Cu
3c. Tableau d’avancement de la réaction :
3d. Calcul de l’avancement maximal :
. . . . . . pour l’oxyde de cuivre : . . xmax = 1,26 . 10-2 /2 = 6,3 . 10-3 mol
. . . . . . pour le carbone : . . x’max = 1,00 . 10-2 mol
donc le réactif limitant est l’oxyde de carbone et l’avancement maximal est : . . xmax = 6,3 . 10-3 mol.
3e. A l’état final, il y a les quantités de matière suivantes :
. . . . . . nCuO = 0 mol
. . . . . . nC = 1,00 . 10-2 - 6,3 . 10-3 = 3,7 . 10-3 mol
. . . . . . nCO2 = xmax = 6,3 . 10-3 mol
. . . . . . nCu = 2 xmax = 1,26 . 10-2 mol.
4a. Avec un bâton d’ébonite chargé négativement, on peut charger S1 négativement par contact.
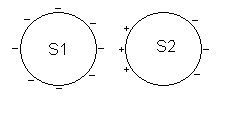
4b. Avec un bâton de verre chargé positivement, on peut charger S1 négativement par influence :
. . . . . . on approche le bâton de verre,
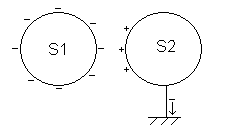
. . . . . . on relie la sphère à la terre,
. . . . . . on supprime le lien vers la terre,
. . . . . . on éloigne le bâton de verre.
4c. Les charges négatives (excédentaires) présentes sur la sphère S1 se repoussent au maximum. Elles sont donc localisées à la surface de la sphère.
4d. A cause du phénomène d’influence, des charges positives apparaissent sur S2 (à proximité de S1) et des charges négatives sont repoussées. Lors de la mise à la terre, des charges négatives (des électrons) vont vers la terre. La sphère S2 devient chargée positivement.
5. Il y a entre les 2 boules électrisées une force de Coulomb telle que : . . F = k (q2)/(d2)
. . . . . . D'où : . . q2 = d2 . `F/k`
. . . . . . D'où : . . q = ± d . `sqrt( F/d )`
. . . . . . A.N. : . . q = ± 4,0 . 10-2 . `sqrt((20 * 10^-3)/(9 * 10^9))` = 6,0 . 10-8 C.
6a. La force d'attraction gravitationnelle s’écrit : . . FS/T = G `(M_S * M_T) /d^2`
. . . . . . A.N. : . . FS/T = 6,67 . 10-11 . `(2,0 * 10^30 * 6,0 * 10^24)/ (150 * 10^9)^2` = 3,6 . 1022 N.
6b. L’homme subit une très forte attraction de la part de la Terre (F = 9,8 . 102 N), d’où son contact avec la Terre. Cette force le cloue au sol !
L’attraction subie de la part du Soleil est 1700 fois plus petite ; malgré l’énorme masse du Soleil, cette force est modérée à cause du très grand éloignement de l’astre.
La force gravitationnelle qui existe entre les humains est négligeable par rapport aux 2 précédentes à cause des faibles masses (comparées à celle de la Terre !) et malgré leur grande proximité (d = 1 m).