D.M.1 du 21/09/10

 

Chimie :

1.a. Le volume d'une sphère de rayon R est : . . V = `4/3` π R³

. . . . A.N. : . . V = `4/3` π (2,0)³ = 34 cm³

 

1.b. Calculons l'encadrement de la valeur du volume V pour : 1,95 cm < R < 2,05 cm.

. . . . D'où : . . `4/3` π (1,95)³ < V < `4/3` π (2,05)³

. . . . A.N. : . . 31,1 cm³ < V < 36,1 cm³

Conclusion : Si le rayon R est exprimé avec 2 C.S., le volume V doit aussi être exprimé avec 2 C.S.

 

1.c. La masse de la sphère de volume V est : . . m = ρ . V

. . . . A.N. : . . m = 2,25 . 34 = 77 g

Remarque : toutes les masses sont exprimées en g et les volumes en cm³.

 

1.d. La quantité de matière n dans la sphère de carbone est : . . n = `m/M`

. . . . A.N. : . . n = `(77)/(12)` = 6,4 mol.

 

1.e. Le nombre d'atomes N dans la sphère de carbone est : . . N = n . N_A

. . . . A.N. : . . N = 6,4 . 6,02 . 10²³ = 3,9 . 10²⁴ atomes.

 

1.f. Lorsque le rayon double, le volume de la sphère est :

V' = `4/3` π R'³ = `4/3` π (2 . R)³ = = 8 . `4/3` π R³ = 8 V.

. . . . D'où : . . m' = 8 m

. . . . . et : . . . n' = 8 n.

. . . . A.N. : . . n' = 8 . 6,4 = 51 mol.

 

 

2.a. Appliquons la relation du gaz parfait au gaz étudié : . . P . V = n . R T

. . . . D'où : . . V = `(n * R * T)/P`

. . . . A.N. : . . V = `(1,00 * 8,31 * 298)/(1020 * 10^2)` = 24,3 . 10^-3 m³ = 24,3 L.

 

2.b. Calculons la valeur du volume à θ' = 100°C . . avec : . . T' = 273 + θ'

. . . . D'où : . . V' = `(n * R * T')/P`

. . . . A.N. : . . V' = `(1,00 * 8,31 * 373)/(1020 * 10^2)` = 30,4 . 10^-3 m³ = 30,4 L.

 

2.c. Calculons la valeur de la pression si le volume est ramené à à sa valeur initiale V.

D'après la relation du gaz parfait : . . P' . V = n . R T'

. . . . D'où : . . P' = `(n * R * T')/V`

. . . . A.N. : . . P' = `(1,00 * 8,31 * 373)/(0,0243)` = 1,28 . 10⁵ Pa = 1,28 . 10³ hPa.

 

 

Physique :

 

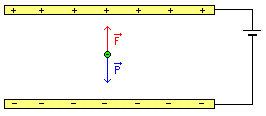
3.a. La gouttelette d’huile électrisée négativement est soumise à 3 forces verticales :

. . . . . . . - son poids `vec{P}` ;

. . . . . . . - l'attraction par la plaque positive `vec{F'}` ;

. . . . . . . - la répulsion par la plaque négative `vec{F''}`.

Remarque : les 2 forces `vec{F'}` et `vec{F''}` sont de même sens quelque soit la polarité des plaques métalliques. Sur les schémas, on a représenté le vecteur `vec{F}` tel que :

`vec{F}` = `vec{F'}` + `vec{F''}`

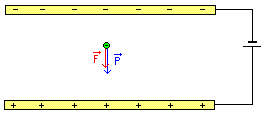
Lorsque le plateau supérieur est chargé positivement, on peut obtenir la situation suivante :

 

 

Pour que la gouttelette reste en équilibre, il faut que l'ensemble des forces électriques qu'elle subit s'oppose à son poids (même direction, même intensité, sens opposés).

Or le poids est vertical descendant, donc les forces électriques doivent être verticales ascendantes.

Les 2 plaques étant chargées, l'une positivement et l'autre négativement, il faut que la plaque inférieure soit chargée négativement (d'où la répulsion de la gouttelette) et la plaque supérieure soit chargée positivement (d'où l'attraction de la gouttelette).

Dans ces conditions, il existe une certaine valeur de la force `vec{F}` pour laquelle la gouttelette reste en équilibre.

Remarque : sur la figure, la force `vec{F}` représente la somme des forces de répulsion de la plaque inférieure et des forces d'attraction de la plaque supérieure.

 

3.b. Lorsqu'on inverse la polarité des plaques métalliques, la gouttelette d’huile électrisée négativement est toujours soumise à 3 forces verticales, mais elles sont, toutes les 3, dirigées vers le bas.

 

 

Dans ces conditions, il est impossible de trouver une position d'équilibre.

 

3.c. L’expérience de Millikan a donc été réalisée dans les conditions de la question 3.a.

 

3.d. Millikan a constaté que les différentes charges q_i portées par la gouttelette ne sont pas quelconques, mais sont toujours telles que :

`(q_1)/5 = (q_2)/7 = (q_3)/4 = (q_4)/8 = (q_5)/6 = (q_6)/3 = (q_7)/8 = (q_8)/4` = ... = q₀ < 0.

ce qui peut aussi s'écrire :

q_i = n_i . q₀ < 0.

Cela montre qu'il existe une charge élémentaire q₀ qui est la charge minimale pouvant être reçue ou cédée par la gouttelette.

Millikan a alors calculé la valeur de la charge élémentaire q₀, et il a obtenu :

q₀ = - 1,6 . 10^-19 C.

Il a alors conclu de ses mesures que la charge d'un électron est : . . e = - 1,6 . 10^-19 C.

L'expérience montre qu'aucune charge plus petite ne peut se manifester au cours d'une expérience d'électrisation.